Now that we finished learning about Python’s major quirks and features, let’s put it into action.
Today, let’s see how to write a “sort” algorithm for lists.
1 Python Built-In Sort Recap
As aforementioned in chapter 5 of this tutorial, Python lists have a built-in list.sort() method that modifies the list in-place.
There is also a sorted() built-in function that builds a new sorted list from an iterable.
sorted() returns a new list, and it doesn’t change the original list:
>>> sorted([5, 2, 3, 1, 4])
[1, 2, 3, 4, 5]
>>> sorted([5, 2, 3, 1, 4], reverse=True)
[5, 4, 3, 2, 1]
Adding reverse=True will sort the list in descending order.
list.sort() method doesn’t return a value, but it changes the list on in-place:
>>> a = [5, 2, 3, 1, 4]
>>> a.sort()
>>> a
[1, 2, 3, 4, 5]
>>> a.sort(reverse=True)
[5, 4, 3, 2, 1]
Same as the sorted() function, list.sort() can also use reverse=True.
It’s worth mentioning that list.sort() only works for lists, but the sorted() function accepts any iterable, and you can define a “key” which is a function that takes a single argument and returns a key to use for sorting purposes. Example:
>>> student_tuples = [
... ('john', 'A', 15),
... ('jane', 'B', 12),
... ('dave', 'B', 10),
... ]
>>> sorted(student_tuples, key=lambda student: student[2]) # sort by age
[('dave', 'B', 10), ('jane', 'B', 12), ('john', 'A', 15)]
Note that there is a new syntax lambda student: student[2]: the lambda keyword defines a new function without a name. The input parameter of the function is student, and the return result is student[2]. So, the above code will sort the student_tuples by each student’s 2nd column (age.)
2 Writing Our Own Sort Function - Bubble Sort
Now that we know how to use sort functions in Python, let’s dive deeper.
How is a sort function implemented? How does it work? How to write one ourselves?
First, let’s try to implement a “bubble sort”:
Bubble sort, sometimes referred to as sinking sort, is a simple sorting algorithm that repeatedly steps through the list, compares adjacent elements, and swaps them if they are in the wrong order. The pass through the list is repeated until the list is sorted. The algorithm, which is a comparison sort, is named for the way smaller or larger elements “bubble” to the top of the list.
It works like this:
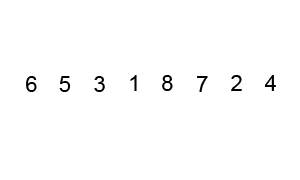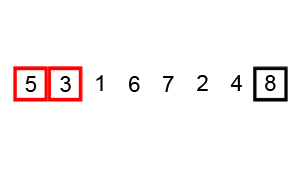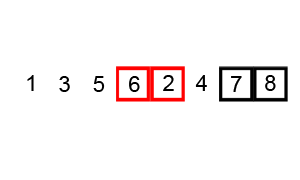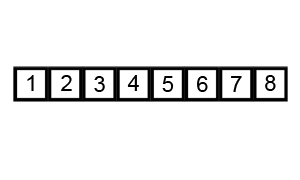
The first pass starts at the first element and ends at the last. After the first pass, the largest element will be moved to the end of the list.
Then the second pass starts at the first element and ends at the second-to-last. After the second pass, the second-largest number will be moved to the second-to-last position on the list.
Now let’s implement that:
def bubble_sort(arr):
n = len(arr)
# the ith round
for i in range(n):
# the last i item has already been in place
for j in range(n-i-1):
# swap if the former one is bigger than the latter
if arr[j] > arr[j+1]:
arr[j], arr[j+1] = arr[j+1], arr[j]
- in the 1st round, there are (n-1) comparisons
- in the 2nd round, there are (n-2) comparisons
- in the last (n-1) round, there is 1 comparison
Average comparisons are (according to the arithmetic sequence’s sum formula): ((n-1) + 1 ) * (n-1) / 2, which is average average complexity of O(n^2).
3 Merge Sort
The bubbles sort algorithm is probably the easiest sort to implement, but it’s not very efficient, since most practical sorting algorithms have substantially better worst-case or average complexity, often O(nlogn).
Let’s look at one of the O(nlogn) algorithms: merge sort.
Merge sort (also commonly spelled as mergesort) is an efficient, general-purpose, and comparison-based sorting algorithm. First, divide the list into the smallest unit (1 element), then compare each element with the adjacent list to sort and merge the two adjacent lists. Finally, all the elements are sorted and merged.
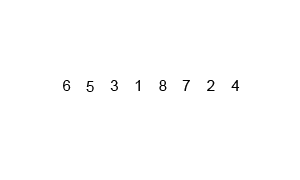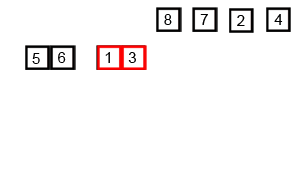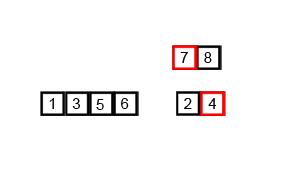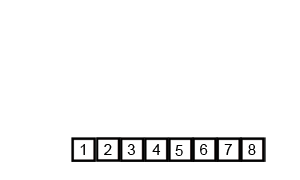
To merge two sorted lists: we compare the first element of each list, take the smaller one, and put it into the result, then loop. When either of the two lists is exhausted, we need to append the other list’s remaining elements to the result.
def merge(l1, l2):
res = []
i, j = 0, 0
while i < len(l1) and j < len(l2):
if l1[i] <= l2[j]:
res.append(l1[i])
i += 1
else:
res.append(l2[j])
j += 1
res = res + l1[i:] + l2[j:]
return res
We use “recursion” (defining a problem in terms of itself) to divide and conquer the merge sort problem:
def merge_sort(l):
if len(l) <= 1:
return l
mid = len(l)//2
l1 = merge_sort(l[:mid]) # recursion
l2 = merge_sort(l[mid:]) # recursion
res = merge(l1, l2)
return res
